点击此处下载文件         2008年河南省中考数学试卷

一、           选择题(本题满分18分，共有6道小题，每小题3分)

下列每小题都给出代号为A、B、C、D的四个答案，其中只有一个是正确的。请将各小题所选答案的代号填写在下面的表格内相应题号下面。

1.－7的相反数是（     ）

A. 7             B. －7           C.                  D. －

2.直角三角形在正方形网格纸中的位置如图所示，则cosα的值是（   ）

A.                  B.               C.                D.    

                           第2题图                                                第3题图         

3.如图，是中国共产主义青年团团旗上的图案，点A、B、C、D、E五等分圆，则∠A＋∠B＋∠C＋∠D＋∠E等于（     ）

4.初三年级某班十名男同学“俯卧撑”的测试成绩（单位：次数）分别是9，14，10，15，7，9，16，10，11，9，这组数据的众数、中位数、平均数依次是（     ）

A. 9，10，11         B.10，11，9         C.9，11，10       D.10，9，11

5.如果关于x的一元二次方程k²x²－(2k＋1) x＋1＝0有两个不相等的实数根，那么k的取值范围是（     ）

A. k＞－     B. k＞－ 且k≠0     C. k＜－       D. k≥－ 且 k≠0

6.如图，已知□ABCD中，AB＝4，AD＝2，E是AB边上的一动点（动点E与点A不重合，可与点B重合），设AE＝x，DE的延长线交CB的延长线于点F，设CF＝y，则下列图象能正确反映y与x的函数关系的是（     ）

二、填空题(本题满分27分，共有9道小题，每小题3分)

7.16的平方根是                        

8.如图，直线a，b被直线c所截，若a∥b，∠1＝50°，则∠2＝          

9.样本数据3，6，a，4，2的平均数是5，则这个样本的方差是          

10.如图所示，AB为⊙O的直径，AC为弦，OD∥BC交AC于点D，若AB＝20cm，∠A＝30°，则AD＝           cm

11.某花木场有一块如等腰梯形ABCD的空地(如图)，各边的中点分别是E、F、G、H，用篱笆围成的四边形EFGH场地的周长为40cm，则对角线AC＝                      cm。

12.如图，矩形ABCD的两条对角线交于点O，过点O作AC的垂线EF，分别交AD、BC于点E、F，连接CE，已知△CDE的周长为24cm，则矩形ABCD的周长是                      cm

13、在一幅长50cm，宽30cm的风景画的四周镶一条金色纸边，制成一幅矩形挂图，如图所示，如果要使整个规划面积是1800cm²，设金色纸边的宽为xcm，那么x满足的方程为                               .

14、如图是二次函数y＝a(x＋1)²＋2图像的一部分，该图在y轴右侧与x轴交点的坐标是                             。

15、如图，直线y＝kx－2 (k＞0)与双曲线 在第一象限内的交点为R，与x轴的交点为P，与y 轴的交点为Q；作RM⊥x 轴于点M，若△OPQ与△PRM的面积是4：1，则k＝                 。

三、解答题(本题满分75分，共8道小题)

16、(本小题满分8分)

解不等式组 并把解集在已画好的数轴上表示出来。

17. (本小题满分9分)

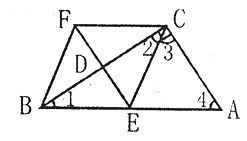
如图，已知：在四边形ABFC中，∠ACB＝90°，BC中的垂直平分线EF交CB于点D，交AB于点E，且CF＝AE

(1)       试探究，四边形BECF是什么特殊的四边形；

(2)       当∠A的大小满足什么条件时，四边形BECF是正方形？请回答并证明你的结论.                       (特别提醒：表示角最好用数字)

18. (本小题满分9分)

已知x₁、x₂是关于x的一元二次方程x²－6x＋k＝0的两个实数根，且    (1) 求k的值；（2）求的值。

19、(本小题满分9分)

某校300名优秀学生，中考数学得分范围是70—119(得分都是整数)，为了了解该校这300名学生的中考数学成绩，从中抽查了一部分学生的数学分数，通过数据处理，得到如下频率分布表和频率分布直方图.

请你根据给出的图标解答：

(1)填写频率分布表中未完成部分的数据；

(2)指出在这个问题中的总体和样本容量；

(3)求出在频率分布直方图中直角梯形ABCD的面积；

(4)请你用样本估计总体，可以得到哪些信息？(写一条即可)

20、（本题满分9分）

在暴雨到来之前，武警某部承担了一段长150米的河堤加固任务，加固40米后，接到上级抗旱防汛指挥部的指示，要求加快施工进度，为此，该部队在保证施工质量的前提下，投入更多的兵力，每天多加固15米，这样一共用了3天完成了任务。问接到指示后，该部队每天加固河堤多少米？

21、（本题满分10分）

如图，在小山的西侧A处有一热气球，以30米/分钟的速度沿着与垂直方向所成夹角为30°的方向升空，40分钟后到达C处，这时热气球上的人发现，在A处的正东方向有一处着火点B，十分钟后，在D处测得着火点B的俯角为15°，求热气球升空点A与着火点B的距离。（结果保留根号，参考数据：

  ( ， ， ， ）。

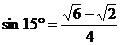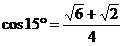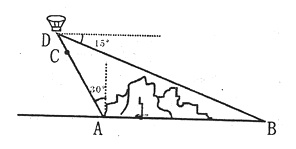
22、（本题满分10分）

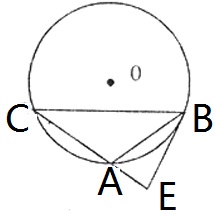
如图，△ABC内接于⊙O，过点B作⊙O的切线，交于CA的延长线于点E，∠EBC＝2∠C.

(1)求证：AB＝AC；(2)当 ＝ 时，①求tan∠ABE的值；②如果AE＝ ，求AC的值。

23、（本题满分11分）

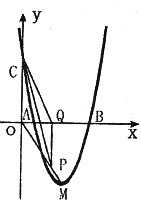
如图，抛物线y＝ax²＋bx＋c与 轴交于A、B两点（点A在点B左侧），与y轴交于点C，且当x＝O和x＝4时，y的值相等。直线y＝4x－16与这条抛物线相交于两点，其中一点的横坐标是3，另一点是这条抛物线的顶点M。

(1)求这条抛物线的解析式；

(2)P为线段OM上一点，过点P作PQ⊥x轴于点Q。若点P在线段OM上运动（点P不与点O重合，但可以与点M重合），设OQ的长为t，四边形PQCO的面积为S，求S与t之间的函数关系式及自变量t的取值范围；

(3)随着点P的运动，四边形PQCO的面积S有最大值吗？如果S有最大值，请求出S的最大值并指出点Q的具体位置和四边形PQCO的特殊形状；如果S没有最大值，请简要说明理由；

(4)随着点P的运动，是否存在t的某个值，能满足PO＝OC？如果存在，请求出t的值。

2008年高级中等学校招生统一考试                    

数学参考答案及评分标准

一、选择题（本题满分18分，共有6道小题，每小题3分）

1.A               2.D                3.B                 4.A                   5.B                   6.B

二．填空题（本题满分27分，共有9道小题，每小题3分）

7.±4； 8. 50； 9. 8   10. 5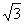    11. 20   12.   13. x²＋40x－75＝0

  14.（1，0） 15.

三．解答题（本大题8个小题，满分75分）

16.（本小题满分8分）解：

解不等式①，得 x≤3·······························3分

解不等式②，得 x＞－1 ·····························6分

把解集在数轴上表示为：

········7分

∴原不等式组的解集是—1＜x≤3···················8分

17.（本小题满分9分）

（1）四边形BECF是菱形。·························1分

证明：EF垂直平分BC，

∴BF＝FC，BE＝EC，∴∠1＝∠2······2分

∵∠ACB＝90°

∴∠1＋∠4＝90°

∠3＋∠2＝90°

∴∠3＝∠4

∴EC＝AE·····················3分

∴BE＝AE··················4分

∵CF＝AE

∴BE＝EC＝CF＝BF··········5分

∴四边形BECF是菱形·······6分

（2）当∠A＝45°时，菱形BESF是正方形··7分

证明：

∵∠A＝45°， ∠ACB＝90°

∴∠1＝45°····························8分

∴∠EBF＝2∠A＝90°

∴菱形BECF是正方形·················9分

18.（本小题满分10分）

解：（1）∵x₁，x₂ 是方程x²－6x＋k＝0的两个根

∴x₁＋x₂ ＝6                   x₁x₂＝k······················1分

∵x x —x —x ＝115

∴k —6＝115·············································2分

解得k ＝11，k ＝－11······································3分

当k ＝11时 ＝36—4k＝36—44＜0 ，∴k ＝11不合题意·······4分

当k ＝－11时 ＝36—4k＝36＋44＞0∴k ＝－11符合题意·········5分

∴k的值为—11············································6分

（2）x ＋x ＝6，x x ＝－11·····························7分

而x ＋x ＋8＝（x ＋x ） —2x x ＋8＝36＋2×11＋8＝66···················9分

19、（本小题满分9分）

（1）根据第一组的频数为15，频率为0.30，

所以这次被抽查的学生人数是

（人）············1分

  第三组的频率为 ·····2分

分数在79.5~89.5之间的人数为50―15―10―18―3＝4人。

频率为 。········3分

因此第二列从上至下 两空分别填4、50；第三列从上至下两空分别填0.36、0.08.····4分

（2）总体是300名学生的中考数学成绩。···············5分

样本容量为50. ·························6分

（3）∵∠DOE＝∠AOF，∠E＝∠AFO＝90°，DE＝AF，

∴△DOE≌△AOF。·······7分

∴S_梯形ABCD＝S_{矩形ABGF＋} S_矩形CDEG＝0.08＋0.36＝0.44. ·······8分

（4）本题有多个结论，例如，300名初中毕业年级学生数学分数在89.5~99.5的人数最多，约为108人；

或300名初中毕业年级学生数学分数在69.5~79.5的人数最少，约为18人。 ······9分

20、（本小题满分9分）

解：设接到指示后，该部队每天加固河堤X米，则接到指示前每天加固（X－15）米········1分

根据题意，得 。················5分

两边乘以X（X－15）得40X＋110（X－15）＝3X（X－15）

整理，得X²－65X＋550＝0. ······················6分

解得，X₁ ＝55，X₂＝10. ·························7分

经检验，X₁ ＝55，X₂＝10都是原方程的根，但当X＝10时X－15＝10－15＜0，

∴X＝10不合题意，只取X＝55。···················8分

答：接到指示后，该部队每天加固河堤55米。········9分

21、（本小题满分10分）

解：由题意可知，AD＝(40＋10)×30＝1500（米）···1分

过点D作DH⊥BA，交BA延长线于点H。·········2分

在Rt△DAH中，DH＝AD·sin60°

＝1500× ＝750 （米）。····4分

AH＝AD·cos60°＝1500× ＝750（米）。·······6分

在Rt△DBH中，

BH＝DH·cot15°＝750 ×(2＋ )＝（1500 ＋2250）（米）···8分

∴BA＝BH－AH＝1500 ＋2250－750＝1500（ ＋1）（米）………..9分

答：热气球升空点A与着火点B的距离为1500（ ＋1）（米）……10分

22、（本小题满分10分）

（1）证明：∵BE切⊙O于点B，

∴∠ABE＝∠C。························1分

∵∠EBC＝2∠C，

即   ∠ABE＋∠ABC＝2∠C。

∴∠ABC＝∠C。

∴AB＝AC。····························2分

（2）解①如图，连接AO，交BC于点F。

∵AB＝AC∴

∴AO⊥BC，且BF＝FC。·······················3分

∵    ∴ ∴ …………………….….…….4分

设 ， ，

由勾股定理，得AF＝ ＝ ………………5分

∴ ……………………………6分

②在 EBA和 ECB中，

∵∠E＝∠E， ∠EBA＝∠ECB，   ∴△EBA∽△ECB，

∴ ＝    ……………………………7分

∵ ＝   

∴ (※)…………………8分

由切割线定理，得

将(※)式代入上式，得 …………………………9分

∵ ，

∴ ………………………………………………10分

23.(本小题满分11分)

解：（1）∵当 和 时， 的值相等，∴ ，……1分

∴ ，∴

将 代入 ，得 ，

将 代入 ，得 ………………………………………….2分

∴设抛物线的解析式为

将点 代入，得 ，解得 .

∴抛物线 ，即 ……………………………..3分

(2)设直线OM的解析式为 ，将点M 代入，得 ，

∴ ……………………………………………………………………..4分

则点P ， ，而 ， .

＝ .......................5分

的取值范围为： ＜ ≤ .......................................6分

(3)随着点 的运动，四边形 的面积 有最大值.

     从图像可看出，随着点 由 → 运动， 的面积与 的面积在不断增大，即 不断变大，显当然点 运动到点 时， 最值...............7分

     此时 时，点 在线段 的中点上............. ................8分

   因而 .

   当 时， ， ∥ ，∴四边形 是平行四边形. ..9分

(4)随着点 的运动，存在 ，能满足 .................10分

     设点 ， ， . 由勾股定理，得 .

     ∵ ，∴ ， ＜ ， (不合题意)

     ∴当 时， ...................................11分