|
版权所有 安阳市超越多媒体学校 联系:13837257994 13623724797(张老师)
|
点击此处下载文件
可下载
安阳市09-10九年级上学期数学期末统考试卷
一、选择题(每题2分,共14分)
1、二次根式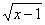
A. x≥1 B.x>1 C.x≥0 D.x>0
2、方程x2=x的解是【 】
A. x=1 B.x=0; C.x1=1,x2=0; D.x1=-1,x2=0;
3、下列各图中既是轴对称图形又是中心对称图形的是【 】
A B C D
4、下列事件中是随机事件的是【】
A. 2012年春节是晴天;
B. 度量一个三角形的三个内角并求和,结果是360°;
C. 度量一个圆中直径所对的圆周角,结果是直角;
D.通常温度降到0℃以下,纯净水会结冰。
5、关于x的方程是一元二次方程程kx2-6x+9=0,则【】
A. k<0 B. k≠0 C. k≥0 D. k>0
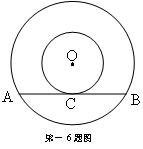
6、如图,两个同心圆的半径分别为3cm和5cm,弦AB与小圆相切于点C,
则AB的长为【】
A. 4cm B. 5cm C.6cm D. 8cm
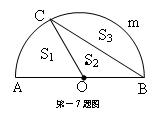
7、如图,AB为半圆O的直径,C是半圆O上一点,且弧AC是半圆的 ,设扇形AOC、
△OBC、弓形BmC的面积分别为S1、S2、S3,下列结论正确的是【】
A. S1<S2<S3 B. S2<S1<S3
C. S2<S3<S1 D. S3<S2<S1
二、填空题(每题2分,共20分)
8、计算: 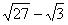
9、计算: 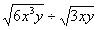
10、一个长方形的长和宽分别是 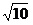
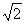
11、方程x2-4x+4=5的根是 .
12、要组织一次篮球联赛,赛制为单循环形式(每两队之间都要赛一场),计划安排15场比赛,应邀请 支球队参加比赛。
13、一个正三角形绕着内心旋转一定角度后图形能和自身重合,这个角度的最小值是 度。
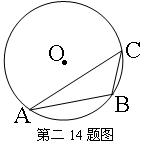
14、如图,△ABC内接于⊙O,∠C=45°,AB=4cm,则⊙O的直径为 cm。
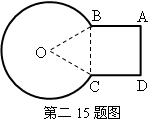
15、一个零件的横截面是由扇形、正三角形、正方形组成,AB=30mm,则这个零部件的横截面的周长是 mm(结果保留π)。
16、已知⊙O的半径是5cm,点P是⊙O外一点,OP=8cm,以P为圆心作一个圆与⊙O相切,这个圆的半径是 cm。
17、同学们,你们都知道猜“石头、剪子、布”的游戏吧!如果你和某同学两人做这个游戏,随机出手一次,你获胜的概率是 。
三、用心解一解(本大题共8个题目,满分66分)
18、(本题6分)计算: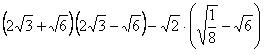
19、(本题6分)用你熟悉的方法解方程: x2-6x-15=0
20、(本题9分)已知关于x 的一元二次方程x2-2x+m=0。
⑴ m取何值时,方程有两个不相等的实数根?
⑵若x=2是原方程的一个根,求此时它的另一个根。
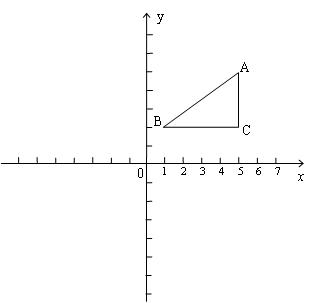
21、(本题9分)如图,在Rt△ABC中,AB=5,BC=4,∠C=90°,点B在平面直角坐标系中的坐标为(1,2)。
⑴画出△ABC关于x轴对称的△A/B/C/的图像。
⑵画出△ABC关于原点对称的△A//B//C//的图像,并写出A//、B//、C//的坐标;
⑶指出△A/B/C/和△A//B//C//的关系是否轴对称或中心对称,若是,指出其对称轴或对称中心。
22、(本题10分)将如图所示的牌面数字1、2、3、4的四张扑克牌背面朝上,洗匀后放在桌面上。
⑴从中随机抽出一张牌,牌面数字是奇数的概率是 ;
⑵从中随机抽出两张牌,两张牌牌面数字的和是6的概率是 ;
⑶先从中随机抽出一张牌,将牌面数字作为十位上的数字,然后将该牌放回并重新洗匀,再随机抽取一张,将牌面数字作为个位上的数字,请用树状图或列表的方法求组成的两位数恰好是3的倍的概率。

23、(本题8分)在平面直角坐标系中,△ABC三个顶点的坐标分别是A(3,6)、B(1,4)、C(1,0)。
⑴△ABC外接圆的圆心坐标是 ;
⑵求以BC为轴,将△ABC旋转一周所得几何体的全面积(即求所有表面的面积之和,结果保留根号和π)
24、(本题8分)某西瓜经营户以2元/千克的价格购进一批小型西瓜,以3元/千克的价格出售,每天可售出200千克。为了促销,该经营户决定降价销售。经调查发现,这种小型西瓜每降价0.1元/千克,每天可多售出40千克,另外,每天的房租等固定成本共24元,该经营户要想每天盈利200元,应将每千克小型西瓜的售价降低多少元?
25、(本题10分)如图,已知⊙O的直径AB的长是4cm,点C在⊙O上,过点C的直径与AB的延长线交于点P,AC=PC,∠COB=2∠PCB。
⑴求证:PC是⊙O的切线;
⑵求弦BC的长。
二、填空题
8、2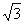
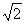
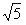
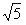
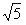
13、120 14、 4 15、(90+50π) 16、3cm或13cm 17、
三、用心解一解
18、解:原式= 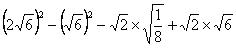
19、解:移项,得 x2-6 x=15
配方,得 x2-6x+9=15+9
(x-3)2=24
开平方,得: x-3=±2
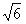
即 x1=3+2
x2=3-2
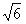
20、解:⑴由题意得△=(―2)2―4m=4-4m
要使方程有两个不相等的实数根,需要△>0
即4-4m>0,解得m<1 所以 m<1,方程有两个不相等的实数根。
⑵ 把x=2代入原方程得,4-4+m=0,解得 m=0,
得到一元二次方程 x2-2 x=0
解得 x1=2,x2=0。即此时它的另外一个根是0
(注:也可以利用根与系数的关系求另一个根)
21、解:⑴ 如图所示
⑵如图所示,A//(-5,-5) B//(-1,-2) C//(-5,-2)
⑶△A/B/C/和△A//B//C//是轴对称关系,对称轴是y轴。
22、解:⑴ 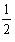
⑶ 列表如下:
|
|
1 |
2 |
3 |
4 |
|
1 |
11 |
12 |
13 |
14 |
|
2 |
21 |
22 |
23 |
24 |
|
3 |
31 |
32 |
33 |
34 |
|
4 |
41 |
42 |
43 |
44 |
其中恰好是3的倍数的有12,21,24,33,42五种结果。所以,P(3的倍数)=
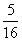
23、解:⑴ (5,2)
⑵旋转后得到的几何体是一个以2为底面半径、6为高的大圆锥,再挖掉一个以2为底面圆的半径、2为高的小圆锥。
它们的母线之长分别为AC=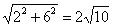
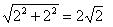
所求全面积为: π·2·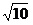
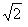 =4
=4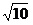
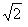 π
π
24、解:设应将每千克小型西瓜的售价降低x元,根据题意得
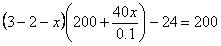
解之得:x1=0.2,x2=0.3
答:将每千克小型西瓜的售价降低0.2或0.3元。
25、解:⑴ ∵ OA=OC
∴ ∠A=∠ACO
又∵ ∠COB=∠A+∠ACO,
∴ ∠COB=2∠A
又∵ ∠COB=2∠PCB
∴ ∠A=∠ACO=∠PCB
∵ AB是⊙O的直径
∴ ∠ACO+∠OCB=90°
∴ ∠PCB+∠OCB=90°
∴ 即OC⊥CP
而OC是⊙O的半径,
∴ PC是⊙O的切线。
⑵ ∵ AC=PC
∴ ∠A=∠P
∵ ∠A=∠ACO=∠PCB
∴ ∠A=∠ACO=∠PCB=∠P
又∵ ∠COB=∠A+∠ACO,∠CBO=∠P+∠PCB
∴ ∠COB=∠CBO
∴ BC=OC
∴ BC=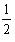 ×4=2(cm)
×4=2(cm)
 最新评论
最新评论|
版权所有 安阳市超越多媒体学校 联系:13837257994 13623724797(张老师)
|