|
版权所有 安阳市超越多媒体学校 联系:13837257994 13623724797(张老师)
|
【例1】、如图,抛物线y=ax2+bx+c与x轴的一个交点A在点(-2,0)和(-1,0)之间(包括两点),顶点C是矩形DEFG上(包括边界和内部) 的一个动点,则⑴abc 0 (填">"或"<") ⑵(★★★)a的取值范围是 。
解:⑴由开口方向 ,得 a<0 由抛物线与y轴的交点知 c>0
由对称轴的位置知 b>0 “左同右异”
即 【对称轴在y轴的左侧a、b同号,对称轴在y轴的右侧a、b异号。】
综上所述知 abc<0
⑵由于是判断a的取值范围,a由抛物线的开口方向和开口程度来表示,由条件可知:
①由图可知,开口最大的是抛物线过点(-2,0),顶点是(3,2),
(注:这是较难理解的,如果你不理解的话,请你自己画画图,再想一想)
因此,只要解出此时的a值就是a的最大值。
设此时的抛物线为y=a(x-3)2+2,将点(-2,0),
代入可求出 a最大=-
②由图可知,开口最小的是抛物线过点(-1,0),顶点是(1,3),
(注:这也是较难理解的,也请你自己画画图,再想一想。)
因此,只要解出此时的a值就是a的最小值。
设此时的抛物线为y=a(x-1)2+3,将点(-1,0),
代入可求出 a最小=-![]()
综上所述知 -![]() <a<-
<a<-
【例2】、小明从如图所示的二次函数的图象中,观察得出下列五条信息:
①c<0; ②abc>0; ③a-b+c>0;(★) ④2a-3b=0;(★) ⑤c-4b>0。(★★★)
你认为其中正确的信息的个数为【 】
A、2; B、3; C、4; D、5。
解:⑴由开口方向,得 a>0 由抛物线与y轴的交点知 c<0 ①√
由对称轴的位置知 b<0 “左同右异”
即 【对称轴在y轴的左侧a、b同号,对称轴在y轴的右侧a、b异号。】
综上所述知 abc>0 ②√
⑵ 当x=-1时,由图象可知: y=a-b+c>0 ③√
⑶由对称轴公式和对称轴的位置可知:x=
2a+3b=0 ④“×”
(注:也可以由a、b符号可知,2a-3b>0来判断 ④“×”)
⑷当x=2时,由图象可知:y=4a+2b+c>0
由对称轴可得:2a=-3b ∴ 4a=-6b
y=4a+2b+c=-6b +2b+c>0 即 c-4b >0 ⑤“√”
综上所述知 :①②③⑤正确,④错误 故选“C”
【例3】、已知二次函数y=ax2+bx+c的图象如图所示,有下列五个结论:
①abc>0; ②b<a+c; ③4a+2b+c>0 ④2c<3b; ⑤a+b>m(am+b),( m≠1的实数)。
其中正确的结论有【 】:(A)、2个 (B)、3个 (C)、4个 (D)、5个
解:⑴由开口方向,得 a<0 ,由抛物线与y轴的交点知 c>0
由对称轴的位置知 b>0 “左同右异”
∴ abc<0 ① ×
⑵ 当x=-1时,由图象可知: y=a-b+c<0 即 a+c<b ② ×
⑶由抛物线的对称性及抛物线与x轴的左交点可知,抛物线与x轴的右交点大于2。
因此,当x=2时,由图象可知:y=4a+2b+c>0
③ “√”⑷由对称轴公式:x==1 ∴a=-
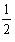
当x=-1时,由图象可知: y=a-b+c<0
将a=-b代入上式,得:y=-
b-b+c<0
化简,得 2c<3b ④“√”
⑸当x=m( m≠1的实数),y=am2+bm+c=m(am+b)+c
∵当x=1时,y最大=a+b+c
∴ y最大>y
即a+b+c>m(am+b)+c
∴ a+b>m(am+b) ( 其中m≠1的实数) ⑤“√”
综上所述:故选“B”
 最新评论
最新评论|
版权所有 安阳市超越多媒体学校 联系:13837257994 13623724797(张老师)
|