|
版权所有 安阳市超越多媒体学校 联系:13837257994 13623724797(张老师)
|
⑴直接开平方法; ⑵配方法; ⑶运用公式法; ⑷因式分解法
⑴ 直接开平方法适用的类型:
ax2=c;(ax+b)2=c;a(mx+n)2=c;(ax+b)2=(mx+n)2
⑵ 配方法适用的类型:
最适合二次项系数是1,一次项系数是偶数的情形。如:x2+2x-8=0
⑶ 运用公式法适用的类型:
将一元二次方程整理成一般形式以后,如果十字相乘法和配方法不方便时,常采用公式法,它适用于一切一般形式的一元二次方程。
⑷ 因式分解法适用的类型:
各类考试中只要是一元二次方程的求解题,首先要考虑因式分解法,特别是一般形式可以用十字相乘法时,是最快捷的方法,但要求同学们对其方法要熟练掌握。其次,可以考虑提公因式和运用公式进行分解因式,无论是怎样可以分解,都要首选因式分解法,此方法不方便时,再考虑其它方法,如求根公式法。
下面就对上述归纳,通过以下例题具体讲解,相信你通过阅读此篇文章,在理解其精髓的基础上对一元二次方程的解法,将会有一个飞跃式的提高。
【例1】 解方程:x2+3x+1=0
分析:此题用十字相乘法无法分解,又不适合用配方法,因此,选用公式法来求解是最佳选择。
解:∵ △=32-4×1×1=5
∴ 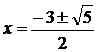
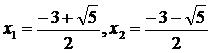
练习:解方程:⑴ x2+4x-5=0 ⑵ 2x2-7x+3=0
解:⑴ 方法一:用十字相乘法是最佳选择,可分解为
(x-1)(x+5)=0 因此,可得根为:x1=1,x2=-5
方法二:由于本题“二次项系数是1,一次项系数是偶数”
用配方法也是比较理想的解法,解答如下:
移项,得 x2+4x=5
配方,得 x2+4x+4=5+4
(x+2)2=9
x+2=±3
因此,可得根为:x1=1,x2=-5方法三:由于许多同学对十字相乘法不熟悉,或没有学会,并且认为配方法比较麻烦,因此,做题中不少同学运用公式法。
∵ △=42+4×1×5=36
∴
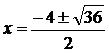
因此,可得根为:x1=1,x2=-5
⑵ 2x2-7x+3=0
方法一:用十字相乘法是最佳选择,可分解为
(x-3)(2x-1)=0 因此,可得根为:x1=3,x2=0.5
方法二:配方法计算量特别大,因此,其次的选择就是求根公式。
∵ △=49-4×2×3=25
∴ 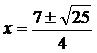
因此,也较容易地求得两根为:x1=3,x2=0.5
【例2】 解方程:2x2-3x-5=0
分析:本题的首选解法是十字相乘法,其次是求根公式法。
方法一:(x+1)(2x-5)=0 因此,可得根为:x1=-1,x2=2.5
方法二:∵ △=9+40=49 因此,可得根为:x1=-1,x2=2.5
练习:解方程:
⑴ 2x2-3x+1=0 ⑵ x2-2![]() x+3=0 ⑶x2-x-1=0
x+3=0 ⑶x2-x-1=0
解:⑴ 2x2-3x+1=0
分析:本题的首选解法是十字相乘法,其次是求根公式法。
方法一:(x-1)(2x-1)=0 因此,可得根为:x1=1,x2=0.5
方法二:∵ △=9-8=1 因此,可得根为:x1=1,x2=0.5
⑵ x2-2![]() x+3=0
x+3=0
分析:由于式子的左边正好是完全平方式,因此,本题的首选解法是将左边写成完全平方式,进行因式分解。
方法一:(x-![]() )2=0 因此,可得根为:x1=x2=
)2=0 因此,可得根为:x1=x2=![]()
由于很多同学在解题时不能观察出左边是完全平方式,因此,常采用求根公式法,也是较为理想的方法,并且运算量也不大。
方法二:∵ △=(2![]() )2-4×1×3=0
)2-4×1×3=0
因此,可得根为::x1=x2=![]()
方法三:由于本题“二次项系数是1,一次项系数2![]() 相当于偶数的情形”用配方法也是比较理想的解法,解答如下:
相当于偶数的情形”用配方法也是比较理想的解法,解答如下:
移项,得 x2-2![]() x=-3
x=-3
配方,得 x2-2![]() x+(
x+(![]() )2=3-3
)2=3-3
(x-![]() )2=0 因此,可得根为:x1=x2=
)2=0 因此,可得根为:x1=x2=![]()
配方法和因式分解写成完全平方公式效果相同。
⑶x2-x-1=0
本题因式分解法几乎不可能,配方法也不方便,且由于系数较小,用求根公式法十分容易。相信你自己可以完成。
【例3】 解方程:2x2-5x+2=0
分析:本题的首选解法是十字相乘法,其次是求根公式法。
解:方法一:(x-2)(2x-1)=0 因此,可得根为:x1=2,x2=0.5
方法二:∵ △=25-16=9 因此,可得根为:x1=2,x2=0.5
【例4】 解方程:x2-6x-16=0
分析:本题的首选解法是十字相乘法,其次是配方法,用求根公式由于数较大就不方便了。
方法一:(x-8)(x+2)=0 因此,可得根为:x1=8,x2=-2
方法二:移项,得 x2-6x=16
配方,得 x2-6x+9=16+9
(x-3)2=25
x-3=±5
因此,可得根为:x1=8,x2=-2
【例5】 解方程::2(y-5)2-72=0
分析:本题是典型的运用直接开平方法求解的题,先将常数移到右边,再两边都除以2,将系数化简。
解:整理,得 (y-5)2=36
开平方,得 y-5=±6
〖口诀〗:一边开方不带“±”,另一边开方带上“±”
化为两个一元一次方程: y-5=6或y-5=-6
因此,可求得根为:y1=11,y2=-1
练习: 解方程:⑴ (x+2)2-25=0
解:移项,得 (x+2)2=25
开平方,得 x+2=±5
〖口诀〗:一边开方不带“±”,另一边开方带上“±”
化为两个一元一次方程: x+2= 5 或 x+2=-5
因此,可求得根为:x1=3,y2=-7
 最新评论
最新评论 评论人:[匿名]
时间: [2010/12/5 21:16:19] IP:[125.65.6.3*]
评论人:[匿名]
时间: [2010/12/5 21:16:19] IP:[125.65.6.3*]|
版权所有 安阳市超越多媒体学校 联系:13837257994 13623724797(张老师)
|