【例1】、如图所示，∠A＝50°，∠C＝80°，∠CBP＝∠PBA，∠CDP＝∠PDA，

                               求∠P的度数。

                              →              

解：设∠CBP＝∠PBA＝x° ，∠CDP＝∠PDA＝y°，

由三角形的外角定理可得

∠1＝∠A＋x°＝∠P＋y°

∠2＝∠C＋y°＝∠P＋x°

∴   ∠A＋x°＋∠C＋y°＝∠P＋y°＋∠P＋x°

∴   ∠A＋∠C＝2∠P

∴ ∠P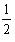＝(∠A＋∠C)＝× (50°＋80°)＝65°

【例2】、如图，已知CD∥AF，∠CDE＝∠BAF，AB⊥BC，∠C＝124°，∠E＝80°，求∠F的度数。

解法1：如图1，延长AB、DC相交于点G。

∵ AB⊥BC，

∴∠CBG＝∠CBA＝90°

∴∠G＝124°－90°＝34°

∵ CD∥AF

∴∠A＝180°－∠G＝180°－34°＝146°                                            

∵∠CDE＝∠BAF＝146°

∴∠F＝720°－146°－90°－124－146°－80°＝134°

（六边形的内角和等于720°）